Rumus-rumus Matematika

Kamis, 04 Desember 2014

RINGKASAN MATERI KALKULUS BAB 3

05.56 No comments

Ringkasan Kalkukus Bab 3

RINGKASAN KALKUKUS BAB 2

05.52 No comments

Ringkasan Kalkulus Bab 1

RINGKASAN KALKULUS BAB 1

05.49 No comments

Ringkasan Kalkulus Bab 1

Ringkasan Materi Kalkulus BAB 0

05.48 1 comment

Ringkasan Kalkukus Bab 0

Materi Matematika SMP Kelas VII

16.13 No comments

Sifat-Sifat Penjumlahan Bilangan Bulat

Untuk menjumlahkan bilangan bulat ada dua cara yang bisa dilakukan yakni menjumlahkan dengan bantuan alat dan menjumlahkan tanpa bantuan. Untuk selengkapnya silahkan baca pada postingan Mafia Online sebelumnya yang berjudul “Operasi penjumlahan bilangan bulat”. Pada postingan ini tidak dibahas lagi mengenai operasi penjumlahan bilangan bulat melainkan sifat-sifat operasi penjumlahan pada bilangan bulat.

Pada penjumlahan bilangan bulat kita akan mengenal lima sifat yakni sifat tertutup, sifat komutatif (pertukaran), mempunyai unsur identitias, sifat asosiatif (pengelompokan), dan mempunyai invers. Untuk penjelasan masing-masing silahkan simak di bawah ini.

Sifat Tertutup

Sifat tertutup maksudnya bahwa pada penjumlahan bilangan bulat, akan selalu menghasilkan bilangan bulat juga. Hal ini dapat dituliskan bahwa “Untuk setiap bilangan bulat a dan b, berlaku a + b = c dengan c juga bilangan bulat”.

Untuk lebih memantapkan pemahaman Anda tentang sifat tertutup pada penjumlahan bilangan bulat, silahkan simak contoh soal di bawah ini.

Contoh Soal 1

a. –7 + 15 = 8

di mana kita ketahui bahwa –7 dan 15 merupakan bilangan bulat dan 8 juga merupakan bilangan bulat.

b. 18 + (–8) = 10

Kita ketahui bahwa bilangan 18 dan –8 merupakan bilangan bulat dan bilangan 10 juga merupakan bilangan bulat.

Sifat Komutatif (Pertukaran)

Penjumlahan dua bilangan bulat selalu diperoleh hasil yang sama walaupun kedua bilangan tersebut dipertukarkan tempatnya. Hal ini dapat dituliskan bahwa “Untuk setiap bilangan bulat a dan b, selalu berlaku a + b = b + a”.

sifat komutatif pada penjumlahan bilangan bulat

Untuk lebih memantapkan pemahaman Anda tentang sifat komutatif (pertukaran) pada penjumlahan bilangan bulat, silahkan simak contoh soal di bawah ini.

Contoh Soal 2

a. 2 + 8 = 8 + 2 = 10

b. (–5) + 4 = 4 + (–5) = –1

c. 6 + (–10) = (–10) + 6 = –4

d. (–11) + (–12) = (–12) + (–11) = –23

Mempunyai Unsur Identitas

Bilangan 0 (nol) merupakan unsur identitas pada penjumlahan. Artinya, untuk sebarang bilangan bulat apabila ditambah 0 (nol), hasilnya adalah bilangan itu sendiri. Hal ini dapat dituliskan bahwa “Untuk sebarang bilangan bulat a, selalu berlaku a + 0 = 0 + a = a.

Sifat Asosiatif (Pengelompokan)

Sifat ini menyatakan bahwa “Untuk setiap bilangan bulat a, b, dan c, berlaku (a + b) + c = a + (b + c).

Untuk lebih memantapkan pemahaman Anda tentang sifat asosiatif (pengelempokan) pada penjumlahan bilangan bulat, silahkan simak contoh soal di bawah ini.

Contoh Soal 3

a. (3 + (–6)) + 7 = –3 + 7 = 4

=> 3 + ((–6) + 7) = 3 + 1 = 4

Jadi, (3 + (–6)) + 7 = 3 + ((–6) + 7).

b. (–2 + (–8)) + 12 = –10 + 12 = 2

=>–2 + ((–8) + 12) = –2 + 4 = 2

Jadi, (–2 + (–8)) + 12 = –2 + ((–8) + 12).

Mempunyai invers

Invers suatu bilangan artinya lawan dari bilangan tersebut. Suatu bilangan dikatakan mempunyai invers jumlah, apabila hasil penjumlahan bilangan tersebut dengan inversnya (lawannya) merupakan unsur identitas yaitu 0 (nol). Invers dari a adalah –a, sedangkan invers dari –a adalah a. Dengan kata lain, untuk setiap bilangan bulat selain nol pasti mempunyai invers, sedemikian sehingga berlaku a + (–a) = (–a) + a = 0.

Sumber
http://dadangjsn.blogspot.com/2013/10/materi-pelajaran-matematika-smp-mts.html

perkalian dan pembagian pecahan

03.44 No comments

Perkalian pecahan

Cara mengalikan pecahan adalah:

Pembilang kali pembilang, penyebut kali penyebut.
Sederhanakan untuk mendapatkan hasil yang sederhana.

Contoh:

$\frac{3}{4}\times\frac{3}{5}=\frac{9}{20}$

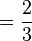
$1\tfrac{2}{3}\times\frac{2}{5}$

=\frac{5}{3}\times\frac{2}{5}

=\frac{1}{3}\times\frac{2}{1}

=\frac{2}{3}

Pembagian pecahan

Cara membagi pecahan adalah:

Ubahlah ke dalam bentuk perkalian dengan kebalikannya.
Lakukan sama seperti perkalian pecahan.

Contoh:

=1\tfrac{3}{4}\div\frac{2}{7}

=\frac{7}{4}\div\frac{2}{7}

=\frac{7x7}{4x2}

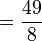
=\frac{49}{8}

=1\tfrac{3}{4}

Subtitusi

17.20 No comments

Rumus Substitusi

Biasanya sering kali ditemukan dalam pelajaran matematika. Rumus Substitusi ini terdapat dalam materi Sistem Persamaan Linear Dua Variabel. Contoh rumusnya adalah : 2x - 3y = 2, 5x + 2y = 24
Rumus Eliminasi
Rumus ini juga termasuk rumus yang terdapat pada Sistem Persamaan Linear Dua Variabel atau lebih singkatnya disebut dengan sebutan SPLDV. Rumus matematika ini lebih gampang cara penyelesaiannya dibandingkan dengan rumus substitusi yang berada di atas, karena caranya lebih singkat dibandingkan dengan rumus subtitusi yang lebih panjang lagi.
y= 1

Dari Wikipedia

Rumus Subtitusi adalah rumus yang digunakan dalam ilmu matematika untuk menyelesaikan suatu persoalan dengan cara menggabungkan persamaan-persamaan yang telah diketahui.

Penyelesaian : 2x - 3y = 2, y = (2x - 2) : 3

Penyelesaian

2x - 3y = 2 . 2

4x - 10y= -8 -

4x - 6y = 4

4x - 10y= -8 -

4y = 4

Selain rumus substitusi dan rumus eliminasi dalam Sistem Persamaan Linear Dua Variabel ini, ada juga rumus penyelesaian SPLDV yang lainnya, yaitu rumus grafika. Rumus grafika ini menggunakan himpunan penyelesaian dan memindahkan himpunan penyelesaian tersebut dalam sebuah grafik yang bernama diagram cartesius yang saat ini sering ditemukan dalam profit/bidang pekerjaan kantoran. Dalam memasukkan himpunan penyelesaian kepada diagram cartesius, angka pertama yang berada dalamhimpunan penyelesaiannya harus dimasukkan dulu atau yang sering kita sebut absis (x) kemudian masukkan angka ordinat (y) ke diagram cartesius yang telah dibuat oleh penggaris

Rumus-rumus Matematika